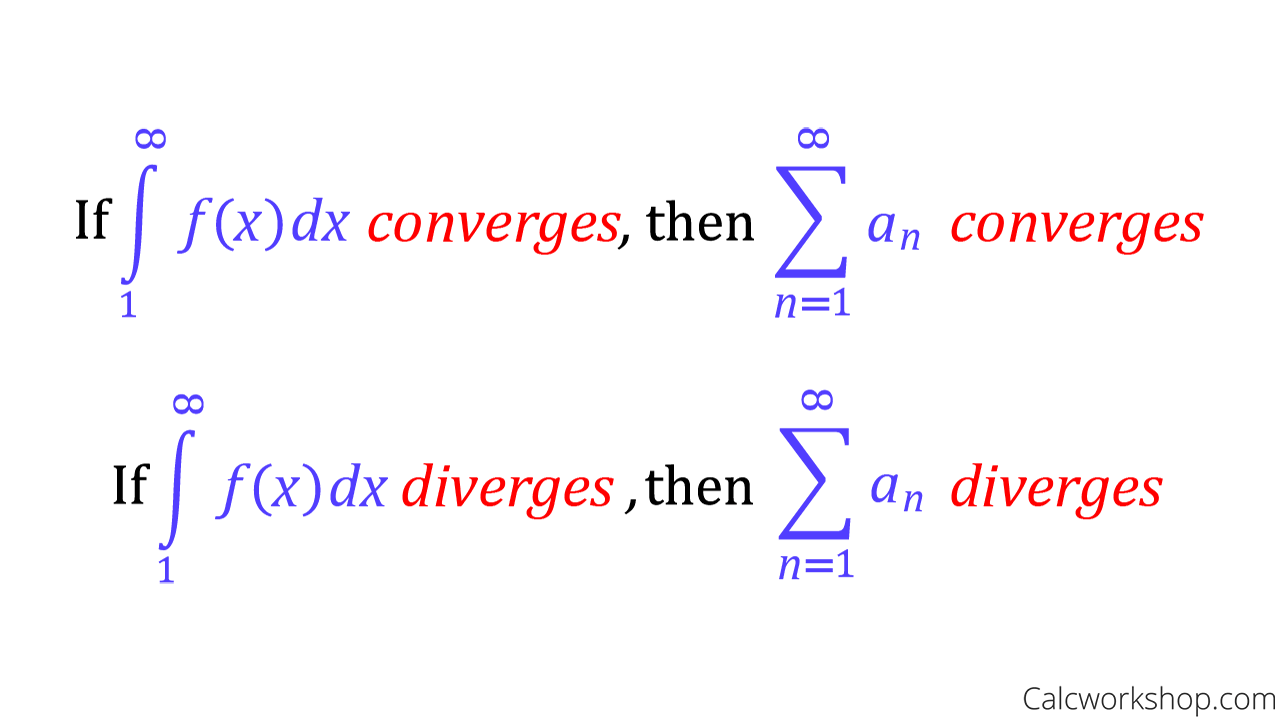Converge In Math

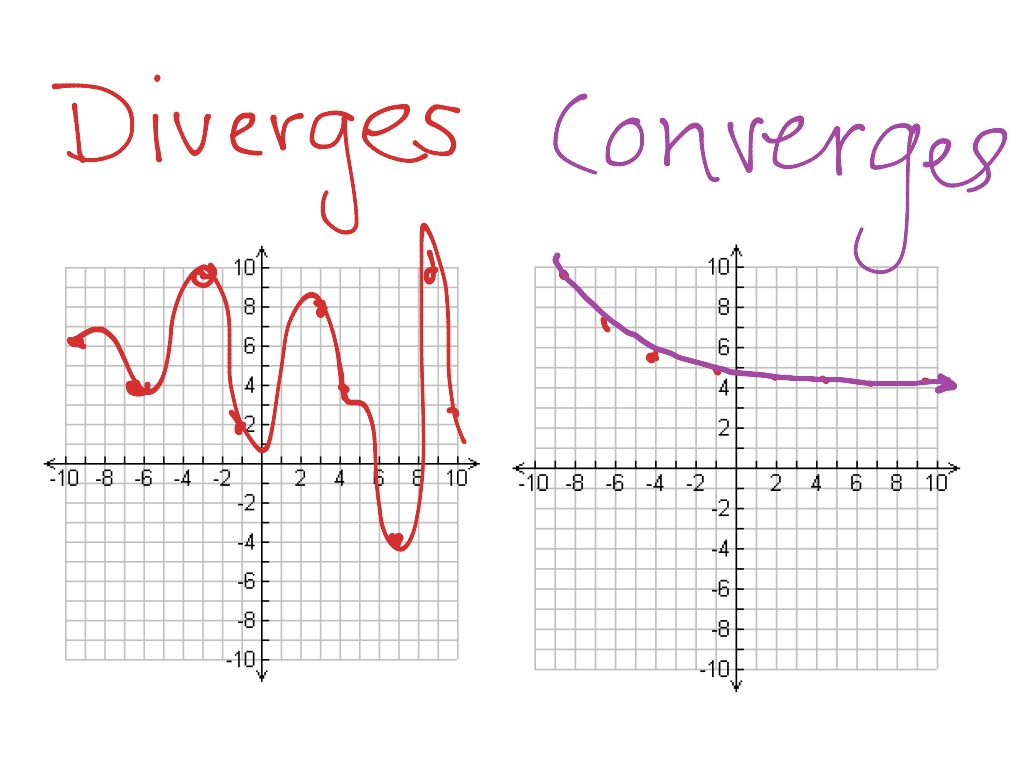
Converge In Math - Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial.

Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial. Something diverges when it doesn't converge.

Something diverges when it doesn't converge. In this section we will discuss in greater detail the convergence and divergence of infinite series. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. We will illustrate how partial. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.

[Resuelta] analisisreal ¿Por qué la convergencia es

We will illustrate how partial. Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In this section we will discuss in greater detail the convergence and divergence of infinite series.

Proving a Sequence Converges Advanced Calculus Example Calculus

In this section we will discuss in greater detail the convergence and divergence of infinite series. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Something diverges when it doesn't converge. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. We will illustrate how partial.

Converging and Diverging Sequences Using Limits Practice Problems

In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.

Week 1 sequence/general term/converge or diverge Math, Calculus

Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In this section we will discuss in greater detail the convergence and divergence of infinite series. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. We will illustrate how partial. Something diverges when it doesn't converge.

Integral Test

Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial. Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.

Higher Maths 1.4 Sequences

Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge. We will illustrate how partial. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity.

All types of sequences in math bkjery

Something diverges when it doesn't converge. In this section we will discuss in greater detail the convergence and divergence of infinite series. We will illustrate how partial. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually.

Sequences Convergence and Divergence YouTube

We will illustrate how partial. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge.

Ex Determine if an Infinite Geometric Series Converges or Diverges

In this section we will discuss in greater detail the convergence and divergence of infinite series. Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. Notoriously the series $$\sum_{k=1}^{\infty} (\frac{1}{n})$$ actually. We will illustrate how partial.

Solved Determine whether the series is convergent or

Notoriously The Series $$\Sum_{K=1}^{\Infty} (\Frac{1}{N})$$ Actually.

Something diverges when it doesn't converge. In mathematics, these concepts describe how a sequence or series behaves as its terms progress towards infinity. We will illustrate how partial. In this section we will discuss in greater detail the convergence and divergence of infinite series.