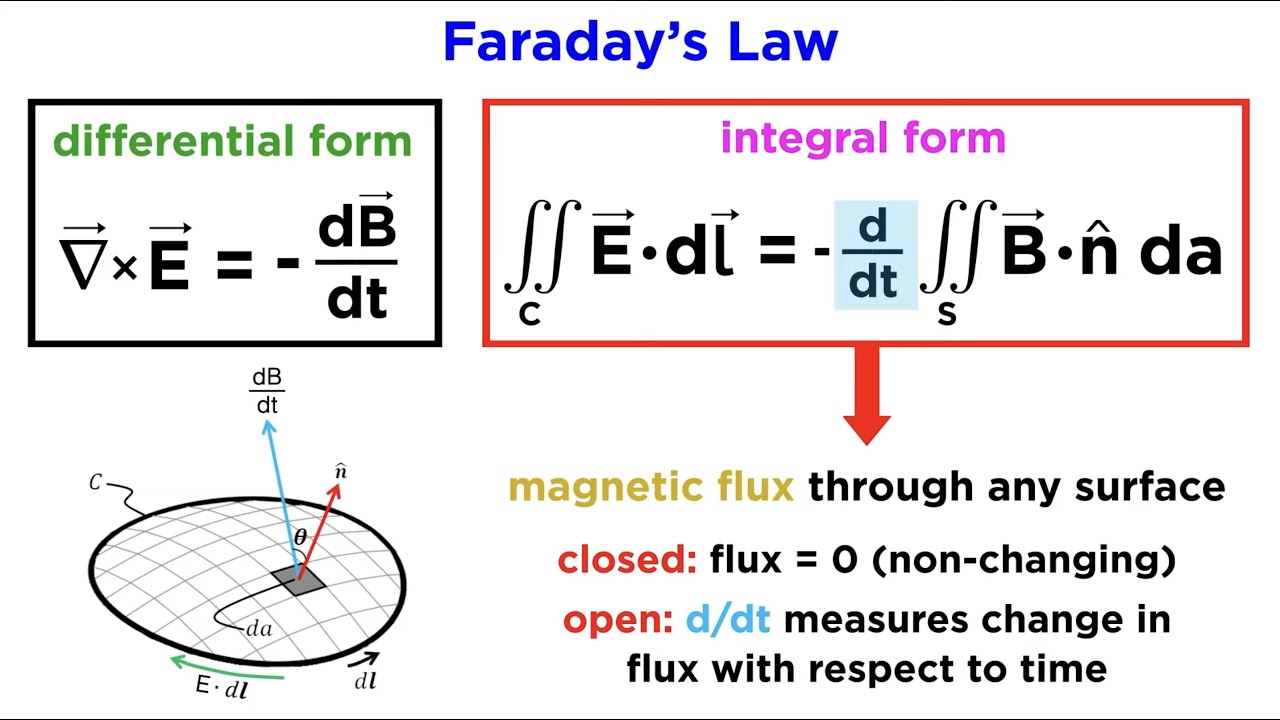
Faraday S Law Integral Form
Faraday S Law Integral Form - The induced emf ε in a coil is proportional to the negative of the rate of change of. Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. I want to understand how stoke's theorem shows that the integral form of faraday's law: Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Faraday’s law of induction may be stated as follows:
Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. Faraday’s law of induction may be stated as follows: I want to understand how stoke's theorem shows that the integral form of faraday's law: Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. The induced emf ε in a coil is proportional to the negative of the rate of change of.
I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. Faraday’s law of induction may be stated as follows: The induced emf ε in a coil is proportional to the negative of the rate of change of. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric.
PPT Faraday’s Law PowerPoint Presentation, free download ID3607741
Faraday’s law of induction may be stated as follows: Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday's law of induction explains that a changing magnetic flux can induce a current in.
Field Integral Equation Derivation Tessshebaylo
Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday’s law.
Maxwell’s Equations Part 3 Faraday’s Law YouTube
Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Faraday’s law of induction may be stated as follows: Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. The induced emf ε in a coil is proportional to the negative.
Faraday's Law Understanding the Alternative (Integral Form)
Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction may.
Solved Derive the differential form of Faraday's law of
Faraday’s law of induction may be stated as follows: I want to understand how stoke's theorem shows that the integral form of faraday's law: The induced emf ε in a coil is proportional to the negative of the rate of change of. Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law.
Faraday's Law Calculations
Faraday’s law of induction may be stated as follows: Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. The induced emf ε in a coil is proportional to the negative of the rate of change of. I want to understand how stoke's theorem shows that the integral.
Solved Maxwell's Equations in a Medium Equations Integral
The induced emf ε in a coil is proportional to the negative of the rate of change of. Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Faraday’s law of induction may be stated as follows: Using stokes’ theorem, this law can be written in integral form as.
Faraday Law, standard (integral form) Physics and mathematics
The induced emf ε in a coil is proportional to the negative of the rate of change of. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday's law of induction explains that a changing magnetic.
Electrical and Electronics Engineering Faraday's Law
Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. The induced emf ε in.
General form of Faraday’s Law
I want to understand how stoke's theorem shows that the integral form of faraday's law: Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. The induced emf ε in a coil is proportional to the negative of the rate of change of. Faraday’s law of induction is a basic law of.
Faraday’s Law Of Induction Is A Basic Law Of Electromagnetism That Predicts How A Magnetic Field Will Interact With An Electric.
Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. I want to understand how stoke's theorem shows that the integral form of faraday's law: Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies.
Faraday’s Law Of Induction May Be Stated As Follows:
The induced emf ε in a coil is proportional to the negative of the rate of change of.