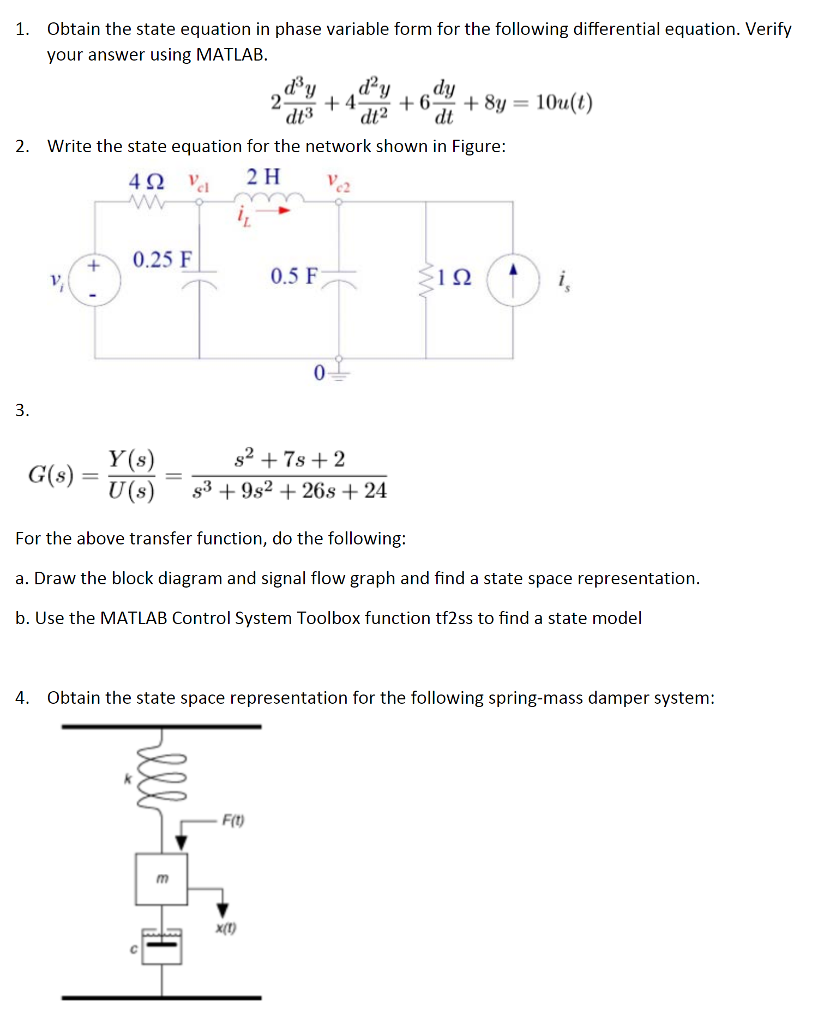
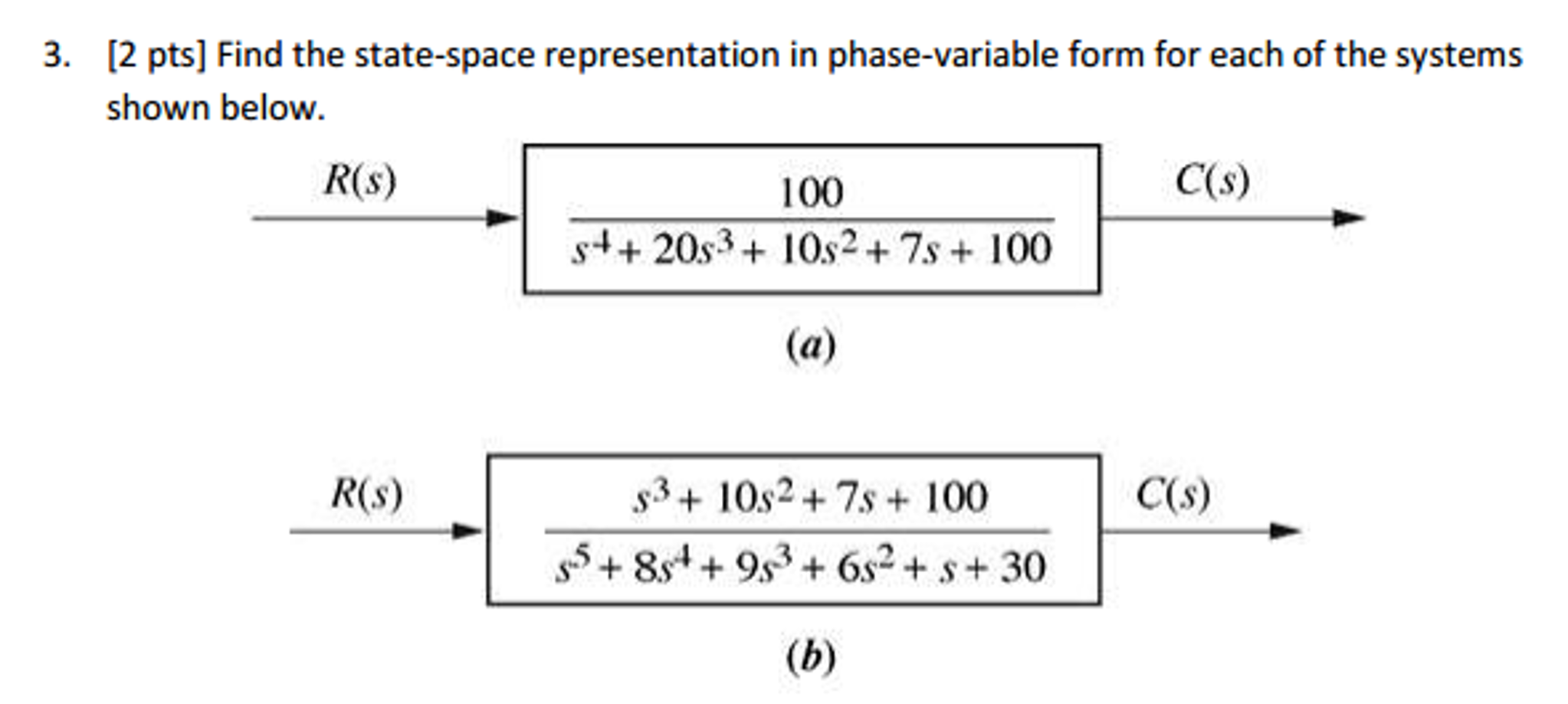
Phase Variable Form
Phase Variable Form - This structure is known as phase variable canonical form (pvcf). It is common to express the state equations in a vector form, in which the set of n state variables is written as a state vector x(t) = [x1(t), x 2(t),. In this form, the coefficients of the characteristic polynomial appear in the last row. The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. If m < n (strictly proper), then bn = 0, ci = bi. The proof follows immediately upon carrying out the indicated change of.
This structure is known as phase variable canonical form (pvcf). In this form, the coefficients of the characteristic polynomial appear in the last row. If m < n (strictly proper), then bn = 0, ci = bi. The proof follows immediately upon carrying out the indicated change of. The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. It is common to express the state equations in a vector form, in which the set of n state variables is written as a state vector x(t) = [x1(t), x 2(t),.
If m < n (strictly proper), then bn = 0, ci = bi. The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. This structure is known as phase variable canonical form (pvcf). It is common to express the state equations in a vector form, in which the set of n state variables is written as a state vector x(t) = [x1(t), x 2(t),. In this form, the coefficients of the characteristic polynomial appear in the last row. The proof follows immediately upon carrying out the indicated change of.
PPT Feedback Control Systems (FCS) PowerPoint Presentation, free
The proof follows immediately upon carrying out the indicated change of. The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. If m < n (strictly proper), then bn = 0, ci = bi. It is common to express the state equations in a vector form, in which the set of n.
State Space Representation in Phase Variable Form Lec2 YouTube
If m < n (strictly proper), then bn = 0, ci = bi. In this form, the coefficients of the characteristic polynomial appear in the last row. The proof follows immediately upon carrying out the indicated change of. It is common to express the state equations in a vector form, in which the set of n state variables is written.
Solved Phase Variable Canonical form (Example1)
The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. The proof follows immediately upon carrying out the indicated change of. In this form, the coefficients of the characteristic polynomial appear in the last row. This structure is known as phase variable canonical form (pvcf). It is common to express the state.
Solved 1. Obtain the state equation in phase variable form
It is common to express the state equations in a vector form, in which the set of n state variables is written as a state vector x(t) = [x1(t), x 2(t),. If m < n (strictly proper), then bn = 0, ci = bi. This structure is known as phase variable canonical form (pvcf). The proof follows immediately upon carrying.
Lecture 3 State Space Canonical forms YouTube
If m < n (strictly proper), then bn = 0, ci = bi. This structure is known as phase variable canonical form (pvcf). In this form, the coefficients of the characteristic polynomial appear in the last row. The proof follows immediately upon carrying out the indicated change of. It is common to express the state equations in a vector form,.
Controllable Canonical Phase Variable Form Method 1 Converting
In this form, the coefficients of the characteristic polynomial appear in the last row. If m < n (strictly proper), then bn = 0, ci = bi. The proof follows immediately upon carrying out the indicated change of. The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. This structure is known.
Solved Find The State Space Representation In Phase Varia...
If m < n (strictly proper), then bn = 0, ci = bi. The proof follows immediately upon carrying out the indicated change of. It is common to express the state equations in a vector form, in which the set of n state variables is written as a state vector x(t) = [x1(t), x 2(t),. In this form, the coefficients.
Phase Variable form from State Space Myacademy YouTube
In this form, the coefficients of the characteristic polynomial appear in the last row. If m < n (strictly proper), then bn = 0, ci = bi. This structure is known as phase variable canonical form (pvcf). The proof follows immediately upon carrying out the indicated change of. It is common to express the state equations in a vector form,.
Feedback Control Systems (FCS) ppt download
The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. In this form, the coefficients of the characteristic polynomial appear in the last row. It is common to express the state equations in a vector form, in which the set of n state variables is written as a state vector x(t) =.
Solved Find the statespace representation in phasevariable
In this form, the coefficients of the characteristic polynomial appear in the last row. The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. This structure is known as phase variable canonical form (pvcf). If m < n (strictly proper), then bn = 0, ci = bi. It is common to express.
It Is Common To Express The State Equations In A Vector Form, In Which The Set Of N State Variables Is Written As A State Vector X(T) = [X1(T), X 2(T),.
This structure is known as phase variable canonical form (pvcf). If m < n (strictly proper), then bn = 0, ci = bi. The phase variable form is obtained simply by renumbering the phase variables in the opposite order of the. In this form, the coefficients of the characteristic polynomial appear in the last row.