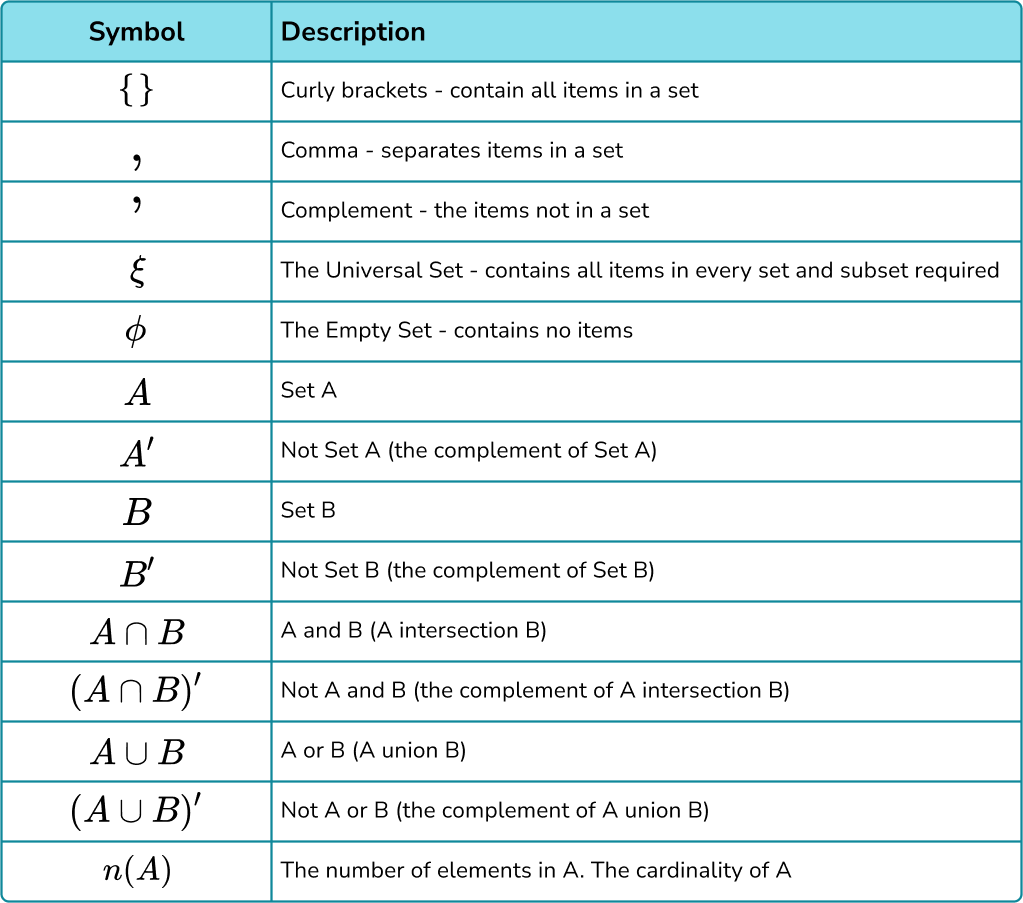
Set Notation Discrete Math
Set Notation Discrete Math - We take the pythonic approach that assumes that starting with zero is more natural than starting at one. This notation is most common in discrete mathematics. A set is a collection of things, usually numbers. We can list each element (or member) of a set inside curly brackets. This is read, “ a is the set containing the elements 1, 2 and 3.”. We need some notation to make talking about sets easier. Consider, a = {1, 2, 3}. For example, the set of natural numbers is defined as \[\mathbb{n} =. For example, the set of natural numbers is defined as \[\mathbb{n} =. In that context the set $s$ is considered to be an alphabet and $s^*$ just.
This is read, “ a is the set containing the elements 1, 2 and 3.”. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. For example, the set of natural numbers is defined as \[\mathbb{n} =. We need some notation to make talking about sets easier. A set is a collection of things, usually numbers. For example, the set of natural numbers is defined as \[\mathbb{n} =. In that context the set $s$ is considered to be an alphabet and $s^*$ just. We can list each element (or member) of a set inside curly brackets. This notation is most common in discrete mathematics. Consider, a = {1, 2, 3}.
Consider, a = {1, 2, 3}. This is read, “ a is the set containing the elements 1, 2 and 3.”. This notation is most common in discrete mathematics. We can list each element (or member) of a set inside curly brackets. For example, the set of natural numbers is defined as \[\mathbb{n} =. We need some notation to make talking about sets easier. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. In that context the set $s$ is considered to be an alphabet and $s^*$ just. A set is a collection of things, usually numbers. For example, the set of natural numbers is defined as \[\mathbb{n} =.
Set Notation Worksheet ⋆
For example, the set of natural numbers is defined as \[\mathbb{n} =. For example, the set of natural numbers is defined as \[\mathbb{n} =. This notation is most common in discrete mathematics. Consider, a = {1, 2, 3}. In that context the set $s$ is considered to be an alphabet and $s^*$ just.
Discrete Mathematics 03 Set Theoretical Operations by Evangelos
For example, the set of natural numbers is defined as \[\mathbb{n} =. A set is a collection of things, usually numbers. For example, the set of natural numbers is defined as \[\mathbb{n} =. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. This notation is most common in discrete mathematics.
Discrete Math Tutorial Examples and Forms
For example, the set of natural numbers is defined as \[\mathbb{n} =. This is read, “ a is the set containing the elements 1, 2 and 3.”. We can list each element (or member) of a set inside curly brackets. A set is a collection of things, usually numbers. In that context the set $s$ is considered to be an.
Different Notations of Sets
We take the pythonic approach that assumes that starting with zero is more natural than starting at one. For example, the set of natural numbers is defined as \[\mathbb{n} =. A set is a collection of things, usually numbers. We can list each element (or member) of a set inside curly brackets. This notation is most common in discrete mathematics.
PPT Discrete Mathematics PowerPoint Presentation, free download ID
This is read, “ a is the set containing the elements 1, 2 and 3.”. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. This notation is most common in discrete mathematics. We need some notation to make talking about sets easier. In that context the set $s$ is considered to.
How To Write In Set Builder Notation
Consider, a = {1, 2, 3}. For example, the set of natural numbers is defined as \[\mathbb{n} =. This is read, “ a is the set containing the elements 1, 2 and 3.”. This notation is most common in discrete mathematics. In that context the set $s$ is considered to be an alphabet and $s^*$ just.
Set Notation GCSE Maths Steps, Examples & Worksheet
We can list each element (or member) of a set inside curly brackets. For example, the set of natural numbers is defined as \[\mathbb{n} =. We need some notation to make talking about sets easier. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. In that context the set $s$ is.
Set Notation GCSE Maths Steps, Examples & Worksheet
This is read, “ a is the set containing the elements 1, 2 and 3.”. In that context the set $s$ is considered to be an alphabet and $s^*$ just. We need some notation to make talking about sets easier. This notation is most common in discrete mathematics. For example, the set of natural numbers is defined as \[\mathbb{n} =.
Set Identities (Defined & Illustrated w/ 13+ Examples!)
For example, the set of natural numbers is defined as \[\mathbb{n} =. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. In that context the set $s$ is considered to be an alphabet and $s^*$ just. A set is a collection of things, usually numbers. This is read, “ a is.
PPT Discrete Mathematics Set Operations and Identities PowerPoint
This notation is most common in discrete mathematics. We can list each element (or member) of a set inside curly brackets. In that context the set $s$ is considered to be an alphabet and $s^*$ just. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. For example, the set of natural.
We Need Some Notation To Make Talking About Sets Easier.
This notation is most common in discrete mathematics. This is read, “ a is the set containing the elements 1, 2 and 3.”. We take the pythonic approach that assumes that starting with zero is more natural than starting at one. In that context the set $s$ is considered to be an alphabet and $s^*$ just.
Consider, A = {1, 2, 3}.
For example, the set of natural numbers is defined as \[\mathbb{n} =. We can list each element (or member) of a set inside curly brackets. For example, the set of natural numbers is defined as \[\mathbb{n} =. A set is a collection of things, usually numbers.