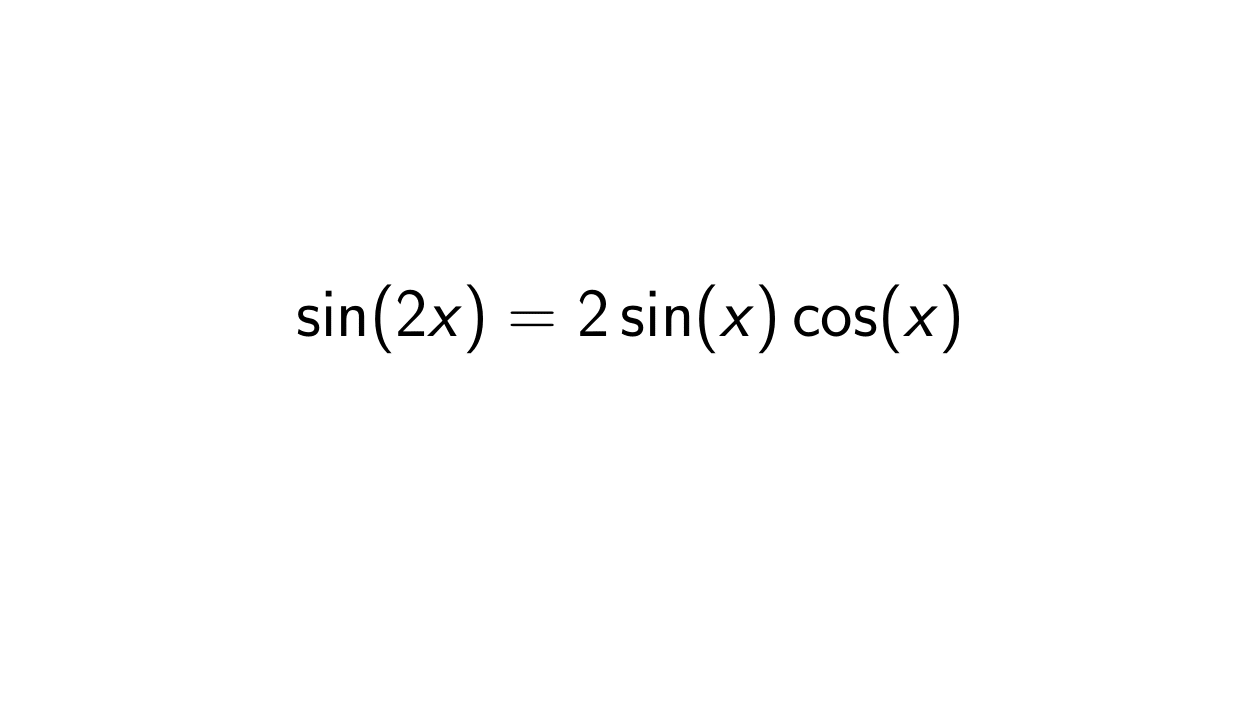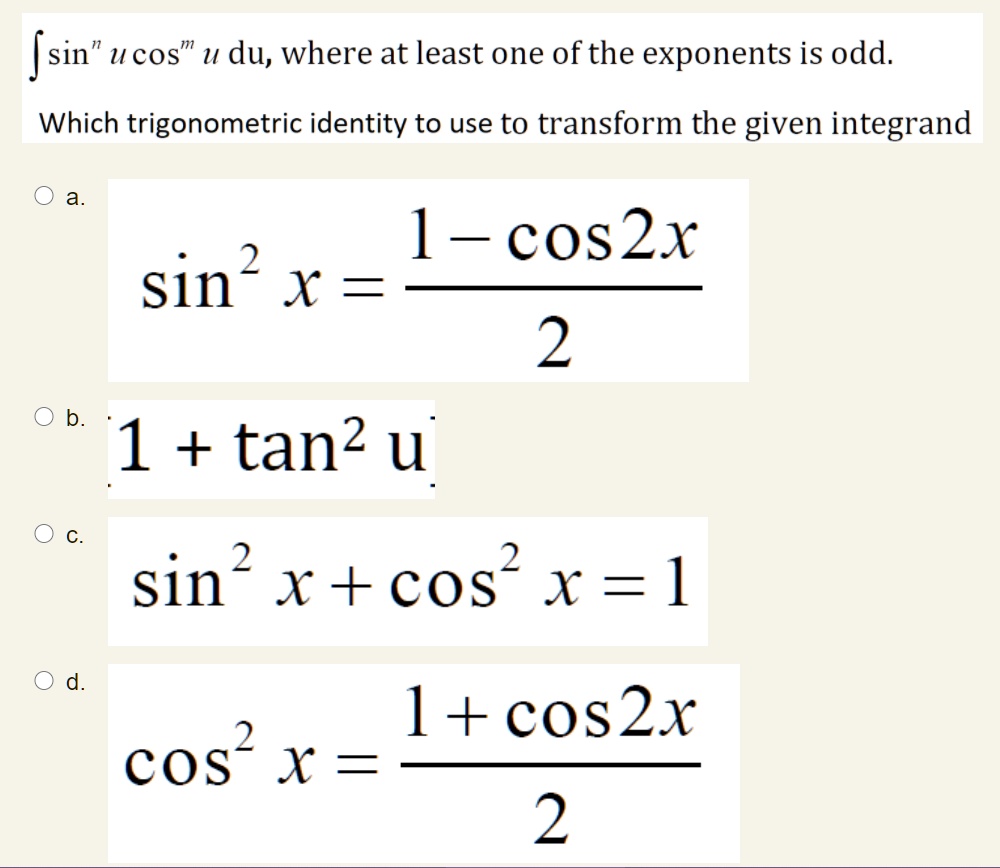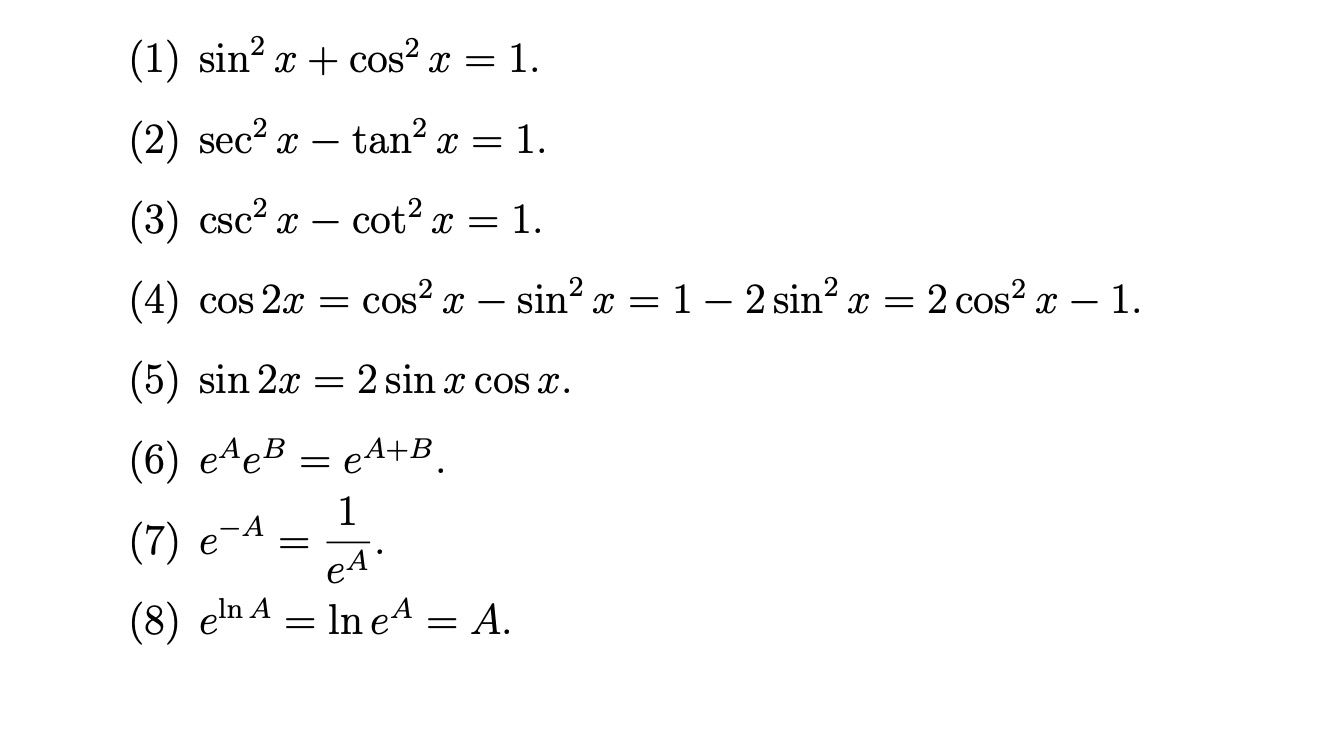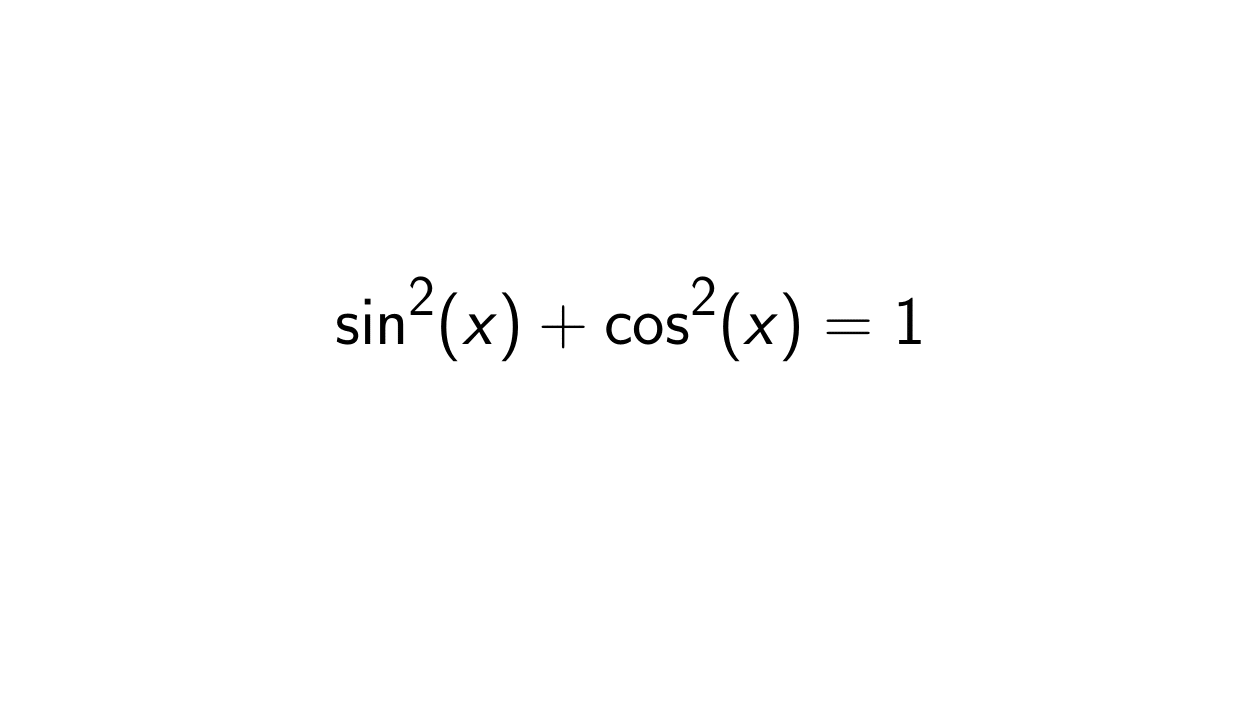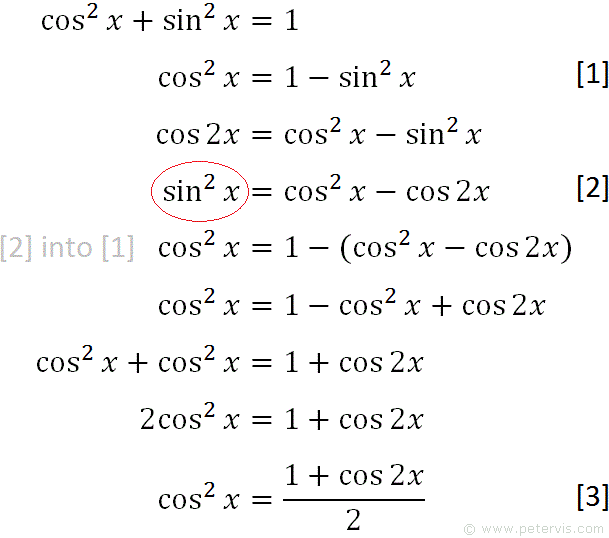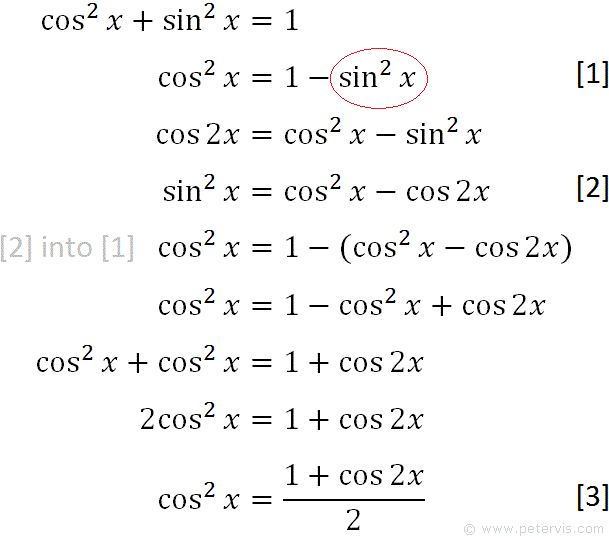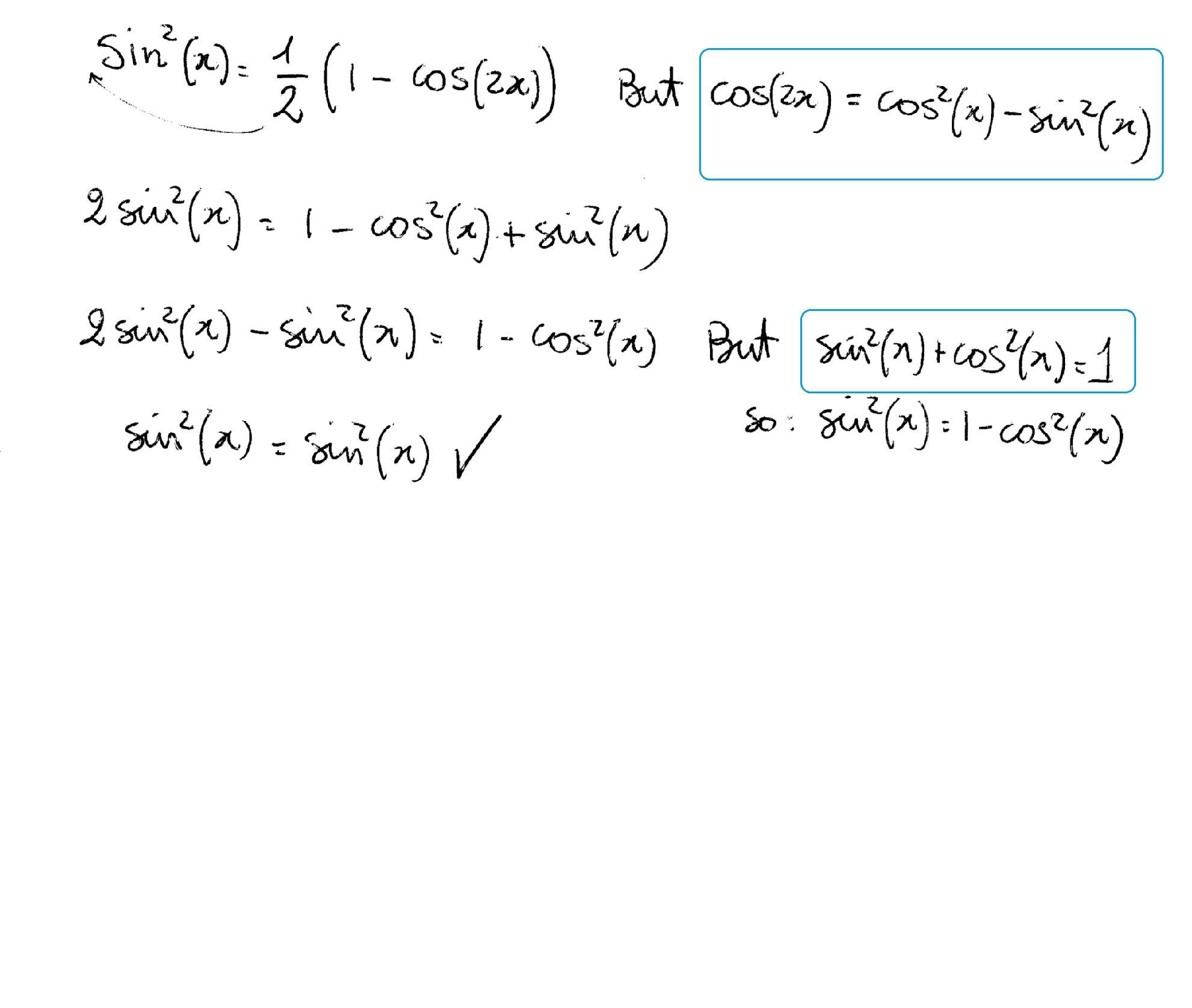Sin 2 Cos 2 1
Sin 2 Cos 2 1 - It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Sin2x +cos2x = 1 ⇒. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values.
The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Sin2x +cos2x = 1 ⇒. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values.
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. Sin2x +cos2x = 1 ⇒. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity:
sin^2(x) + cos^2(x) = 1 Trig Identity Graphical Proof YouTube
The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Sin2x +cos2x = 1 ⇒. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Just as the distance between the origin and any point (x,y) on a.
Sine Formula Triangle
Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: Sin2x +cos2x = 1 ⇒. It so happens that #sin^2(x) + cos^2(x) = 1# is.
Solved Explain what's wrong with this proof since cos^2
Sin2x +cos2x = 1 ⇒. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. It so happens that #sin^2(x) + cos^2(x) = 1# is one of.
Prove that sin(2x) = 2sin(x)cos(x) Epsilonify
Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Sin2x +cos2x = 1 ⇒. Just as the distance between the origin and any point (x,y).
Ex 5.6, 5 Find dy/dx, x = cos cos 2, y = sin sin 2
Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Sin2x +cos2x = 1 ⇒. Replace in the equation cos2x by (1 − sin2x) we know this.
SOLVED Sin U Cos U Du, Where At Least One Of The Exponents, 48 OFF
Sin2x +cos2x = 1 ⇒. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove.
Here is a list of identities involving trigonometric
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Sin2x +cos2x = 1 ⇒. Replace in the equation cos2x by (1 − sin2x) we know this is.
Prove that sin^2(x) + cos^2(x) = 1 Epsilonify
Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) =.
Cos 2 Sin 2 Identity on Sale
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Just as the distance between the origin and any point (x,y) on a circle must be the circle's.
How do you verify sin^2(x) = (1/2)(1cos2x)? Socratic
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Sin2x +cos2x = 1 ⇒. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Just as the distance between the origin and any point (x,y) on a.
Just As The Distance Between The Origin And Any Point (X,Y) On A Circle Must Be The Circle's Radius, The Sum Of The Squared Values.
Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: Sin2x +cos2x = 1 ⇒. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally.