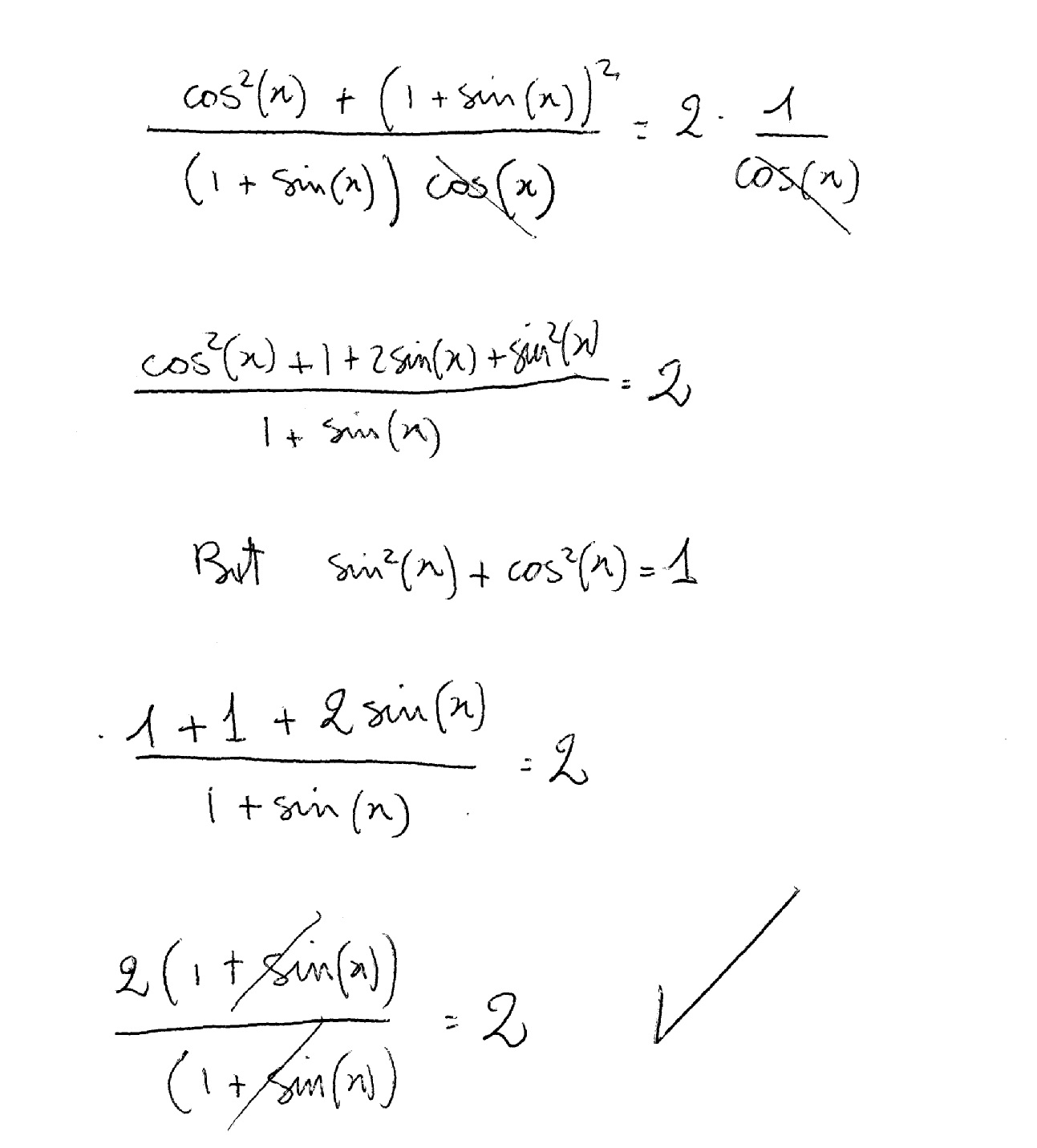What Is Cosx Sinx

What Is Cosx Sinx - We can say it's a sum, i.e = cos x sin x +. Finding the value of cos x sin x: We have, cos x sin x. = 2 cos x sin x 2. Multiplying and dividing the given with 2. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1 cos(2x) = 1.

Finding the value of cos x sin x: Multiplying and dividing the given with 2. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. We can say it's a sum, i.e = cos x sin x +. = 2 cos x sin x 2. We have, cos x sin x. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1 cos(2x) = 1.

Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1 cos(2x) = 1. Finding the value of cos x sin x: = 2 cos x sin x 2. We have, cos x sin x. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. We can say it's a sum, i.e = cos x sin x +. Multiplying and dividing the given with 2.

How do you verify this identity (cosx)/(1+sinx) + (1+sinx)/(cosx

We have, cos x sin x. Finding the value of cos x sin x: = 2 cos x sin x 2. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1 cos(2x) = 1. We can say it's a sum, i.e = cos x.

cosx^2+sinx^2=1

Finding the value of cos x sin x: In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. = 2 cos x sin x 2. We have, cos x sin x. We can say it's a sum, i.e = cos x sin x +.

y=(sinxcosx)^sinxcosx,Find dy/dx for the given function y wherever

We have, cos x sin x. We can say it's a sum, i.e = cos x sin x +. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. Finding the value of cos x sin x: Multiplying and dividing the given with 2.

Misc 17 Find derivative sin x + cos x / sin x cos x

We have, cos x sin x. Finding the value of cos x sin x: Multiplying and dividing the given with 2. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1 cos(2x) = 1. In trigonometry, trigonometric identities are equalities that involve trigonometric functions.

Find the minimum value of sinx cosx ? Brainly.in

We have, cos x sin x. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. Finding the value of cos x sin x: = 2 cos x sin x 2. We can say it's a sum, i.e = cos x sin x +.

Cosxsinx/cosx+sinx simplify? YouTube

= 2 cos x sin x 2. We have, cos x sin x. Finding the value of cos x sin x: We can say it's a sum, i.e = cos x sin x +. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables.

Prove that sinx. Tanx/1cosx=1 secx? EduRev Class 11 Question

We can say it's a sum, i.e = cos x sin x +. We have, cos x sin x. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. Multiplying and dividing the given with 2. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle.

Integral of (sinx + cosx)^2 YouTube

Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1 cos(2x) = 1. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. = 2 cos x sin x 2. We have, cos x.

If y = (cosx + sinx)(cosx sinx) , prove that dydx = sec^2 (x + pi4 )

= 2 cos x sin x 2. We can say it's a sum, i.e = cos x sin x +. Multiplying and dividing the given with 2. We have, cos x sin x. Finding the value of cos x sin x:

Find the derivatives of sinx cosx Yawin

Multiplying and dividing the given with 2. We can say it's a sum, i.e = cos x sin x +. We have, cos x sin x. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle.

Finding The Value Of Cos X Sin X:

Multiplying and dividing the given with 2. = 2 cos x sin x 2. We have, cos x sin x. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1 cos(2x) = 1.